古纯果乐抓电子游艺规则,古纯果乐抓电子游戏技巧
我利用Python代码分析赌场套路,在我们村里打牌再也没输过了!
◀◀◀点击图片进入游戏————◀◀◀◀———点击图片进入游戏———网上真钱游戏,赌钱网站,棋牌游戏平台

软件开发的概念。
Python 编程语言内部二进制代码放大镜
私信小编007即可自动获取大量Python视频教程以及各类PDF!
今天,有个小伙伴神秘兮兮地问我:“有什么地方玩得好,吃得好,睡得好,而且不用花钱,最好还能赚钱?”
看着我一脸蒙圈的样子,小伙伴一本正经地给出了回答:“打个飞的去拉斯维加斯一趟,所有的博彩游戏,都离不开概率这一核心问题,所以只要了解概率是怎么一回事,那么一定能够制胜。
”
咦,统计模拟方法不就是得名于著名赌城蒙特卡罗么!这设想简直棒呆!有概率论知识和蒙特卡罗模拟的技能傍身,幸运小转盘那么一转,小钱钱们排着队向我们招手!
话不多说,我们赶紧开始吧!
先看看一个简单的对赌游戏。
抛硬币游戏:正反两面概率各50%,正面你赢,反面庄家赢。
每次下注1元,赔率1:1(净赔率,意思是下注1元,如果你赢了得2元,赢1元;输了,赔1元)。
这是一个绝对公平的游戏,庄家和闲家胜率各半。
首先,我们模拟10位玩家,每位玩家赌本10元,进行100轮游戏,破产即退出,看看结果怎样。
抛硬币游戏:
抛硬币,正反两面概率各50%,正面你赢,反面庄家赢。
10位玩家,赌本10元,进行100轮。
sample_list = []
round_num = 100
person_num = 10
for person in range(1,person_num+1):
gambling_money = 10
for r in range(1,round_num+1):
coin = random.randint(0, 1) # 0为正,1为反
if coin == 0 :
gambling_money = gambling_money + 1
elif coin == 1 :
gambling_money = gambling_money - 1
if gambling_money == 0 :
sample_list.append([person,r,gambling_money])
break
else:
pass
sample_list.append([person,r,gambling_money])
sample_data1 = pd.DataFrame(sample_list,columns=[person,round,gambling_money])
sample_data1.to_csv(./十元赌本进行100轮游戏.csv,index=0)
看下结果:
*从左到右分别是轮数排序,轮数,结束时持有金钱。
结果显示,赢得最多的玩家赢了24元,而有6位玩家宣告破产(红条),其中运气最差的只玩了28轮。
似乎感觉哪里有点不对~我们换个规则:
100位玩家,赌本10元,1000轮。
抛硬币游戏:
抛硬币,正反两面概率各50%,正面你赢,反面庄家赢。
100位玩家,赌本10元,进行1000轮。
sample_list = []
round_num = 1000
person_num = 100
for person in range(1,person_num+1):
gambling_money = 10
for r in range(1,round_num+1):
coin = random.randint(0, 1) # 0为正,1为反
if coin == 0 :
gambling_money = gambling_money + 1
elif coin == 1 :
gambling_money = gambling_money - 1
if gambling_money == 0 :
sample_list.append([person,r,gambling_money])
break
else:
pass
sample_list.append([person,r,gambling_money])
sample_data2 = pd.DataFrame(sample_list,columns=[person,round,gambling_money])
sample_data2.to_csv(./十元赌本进行1000轮游戏.csv,index=0)
结果奉上: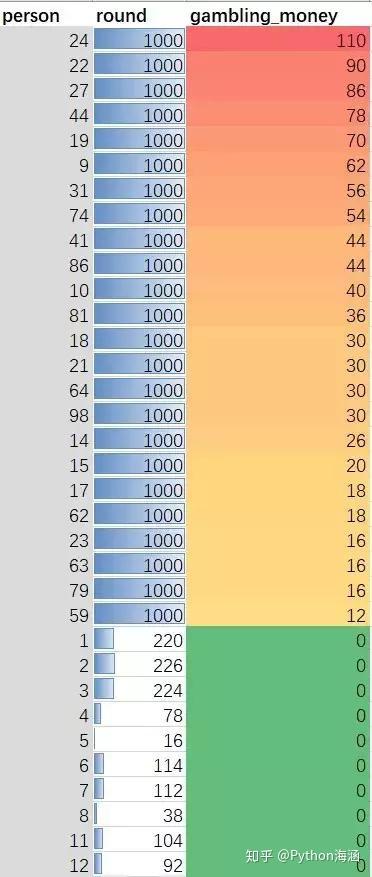
100位玩家中,只有24位玩家没有破产,第一幸运儿赢了10倍,而绝大多数玩家倾家荡产。
此刻,我那位萌萌哒的小伙伴陷入了困惑,问了一个很有哲理的问题:这是一个公平的游戏,但是看结果,我好像很大可能会破产?
再来!100位玩家,赌本10元,破产时结束游戏。
抛硬币游戏:
抛硬币,正反两面概率各50%,正面你赢,反面庄家赢。
100位玩家,赌本10元,进行无限轮,直到破产。
sample_list = []
person_num = 100
t1 = time.time()
for person in range(1,person_num+1):
gambling_money = 10
r = 0
while gambling_money > 0 :
r += 1
print(进行第{}轮游戏.format(r))
coin = random.randint(0, 1) # 0为正,1为反
if coin == 0 :
gambling_money = gambling_money + 1
elif coin == 1 :
gambling_money = gambling_money - 1
if gambling_money == 0 :
sample_list.append([person,r,gambling_money])
break
else:
pass
t2 = time.time()
t = round(t2 - t1,2)
print(t,秒)
sample_data3 = pd.DataFrame(sample_list,columns=[person,round,gambling_money])
sample_data3.to_csv(./十元赌本进行无限轮游戏.csv,index=0)
结果是: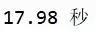
模拟结束。
最坚挺的玩家玩了28706轮,最懵逼的玩家只玩了10轮!
解释一下,意思就是这个人玩抛硬币游戏,连续抛10次,都是反面。
而这一事件发生的概率是0.5的10次方= 1/1024,比千分之一的概率还小。
如下图所示:玩家平均在55轮宣告破产,在第256轮,有一半玩家破产,曲线随着轮数的增加趋于平缓,但无限向100%逼近。
(增加样本数量可以使图更精确)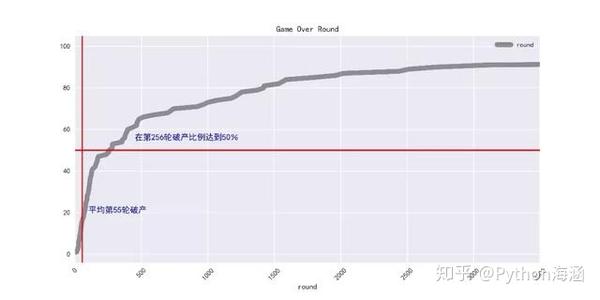
结果一出来,小伙伴怒了!
怀疑我出老千。
好吧!为了公平起见,重新设置游戏规则如下:
100000位玩家,赌本10元,庄家赌本10元,对赌,直到一方破产。
聪明的你一定算出来了,双方破产的概率均为50%~来看看我有木有背地里出老千:
抛硬币游戏:
抛硬币,正反两面概率各50%,正面你赢,反面庄家赢。
100000位玩家,赌本10元,庄家赌本10元,对赌,直到一方破产。
sample_list = []
person_num = 100000
for person in range(1,person_num+1):
gambling_money_dealer = 10
gambling_money_player = 10
r = 0
while 1:
r += 1
print(第{}位玩家,进行第{}轮游戏.format(person,r))
coin = random.randint(0, 1) # 0为正,1为反
if coin == 0 :
gambling_money_player = gambling_money_player + 1
gambling_money_dealer = gambling_money_dealer - 1
elif coin == 1 :
gambling_money_player = gambling_money_player - 1
gambling_money_dealer = gambling_money_dealer + 1
if (gambling_money_player == 0) or (gambling_money_dealer ==0):
sample_list.append([person,gambling_money_dealer,gambling_money_player,r])
break
sample_data4 = pd.DataFrame(sample_list,columns=[person,dealer,player,round])
sample_data4.to_csv(./庄家和闲家各十元赌本对赌直到一方破产.csv,index=0)
结果是50150个庄家破产,49850个玩家破产,符合预期。
说明模拟是正确的,那么问题在哪呢?
重新玩:100000位玩家,赌本10元,庄家赌本20元,对赌,直到一方破产。
这回,我们给庄家20元赌本,看看会发生什么?
抛硬币游戏:
抛硬币,正反两面概率各50%,正面你赢,反面庄家赢。
100000位玩家,赌本10元,庄家赌本20元,对赌,直到一方破产。
sample_list = []
person_num = 100000
for person in range(1,person_num+1):
gambling_money_dealer = 20
gambling_money_player = 10
r = 0
while 1:
r += 1
print(第{}位玩家,进行第{}轮游戏.format(person,r))
coin = random.randint(0, 1) # 0为正,1为反
if coin == 0 :
gambling_money_player = gambling_money_player + 1
gambling_money_dealer = gambling_money_dealer - 1
elif coin == 1 :
gambling_money_player = gambling_money_player - 1
gambling_money_dealer = gambling_money_dealer + 1
if (gambling_money_player == 0) or (gambling_money_dealer ==0):
sample_list.append([person,gambling_money_dealer,gambling_money_player,r])
break
sample_data5 = pd.DataFrame(sample_list,columns=[person,dealer,player,round])
sample_data5.to_csv(./庄家二十元赌本和闲家十元赌本对赌直到一方破产.csv,index=0)
结果如下:
庄家有66723个获胜,玩家有33277个获胜。
获胜比例约为2:1。
这和双方的赌本比例一致。
我们可爱的小伙伴激动了~ 他说,我已经透过现象,洞穿了其中的本质:在赌桌上打倒对方的概率为:我的钱/大家的钱。
好吧~这么浅显的东西其实早有人总结出来了:赌徒输光定理。
在绝对公平的赌博游戏中,最终获胜的概率和双方的资金有关,公式为a/a+b。
可以推断:如果一方拥有无限的资金,那么其获胜概率为100%,另一方破产的概率为100%。

在真实环境中,无限是不存在的,但是我想以你那点微薄的赌资和赌场庞大的资本相比,其实也区别不大了。

不过,总有那么些人,1个亿是小目标,5个亿是零花钱,50个亿是中等意思,这些人来到赌场一掷千金,赌场是不是会破产?
诶~又天真了。
赌场说,我提供你免费的场地玩,免费的房间睡,还有免费的好吃的,你如果赢钱了,就稍微意思意思嘛,比如给我个2%当佣金。
好!某人带着他的小目标就这样玩起了我们喜闻乐见的抛硬币游戏:
正反两面概率各50%,正面你赢,反面庄家赢。
玩家获胜,庄家会抽取2%作为抽成。
模拟100W轮。
抛硬币游戏:
抛硬币,正反两面概率各50%,正面你赢,反面庄家赢。
玩家获胜,庄家会抽取2%作为抽成。
模拟100W轮
sample_list = []
gambling_money_dealer = 0
gambling_money_player = 0
for i in range(1,1000000+1):
print(正在进行第{}轮游戏.format(i))
coin = random.randint(0, 1) # 0为正,1为反
if coin == 0 :
gambling_money_player = gambling_money_player + 0.98
gambling_money_dealer = gambling_money_dealer - 0.98
elif coin == 1 :
gambling_money_player = gambling_money_player - 1
gambling_money_dealer = gambling_money_dealer + 1
sample_list.append([i,gambling_money_dealer,gambling_money_player])
sample_data6 = pd.DataFrame(sample_list,columns=[round,dealer,player])
sample_data6.to_csv(./庄家抽取2%抽成.csv,index=0)
我相信在1,000,000轮的模拟之下,任何套路都无处可藏!
结果是这样的: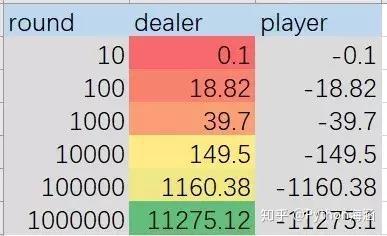
解释一下:2%虽然微小,但却让原本公平的游戏变得不公平,赌场有了2%的优势率。
虽然很小,但奠定了胜局。
这就是我们常说的大数法则:在随机现象的大量重复中往往出现几乎必然的规律。
柯尔莫哥洛夫强大数律:若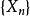
为独立同分布随机变量序列,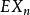
存在,则以概率1成立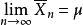
如果对数学过敏,直接看结果:
赌场最终获利0.02*A,所以,只要概率占优,最后获利只跟你总的下注大小有关。
一句话总结:赌的越多,输的越多,十赌九输,久赌必输。
所以说,世界上从来都没有天上掉馅饼的好事,有的只是一夜暴“负”的套路。
那么,究竟有什么地方人少,玩得好,吃得好,睡得好,不用花钱,最好还能赚钱?
有奖竞答
抛硬币游戏,正反两面概率各50%,正面你赢,反面庄家赢。
赔率1:2(假如下注1元,赢了得3元,赚2元),那么每次下注多少比例的资金合适?抛硬币游戏,正反两面概率各50%,每次猜是正面还是反面,赔率1:1(假如下注1元,赢了得2元,赚1元)。
那么如果连续10轮结果都是正面,那么第11轮,你会做何选择?
我利用Python代码分析赌场套路,在我们村里打牌再也没输过了!
*****古纯果乐抓电子游艺规则,古纯果乐抓电子游戏技巧***** *****古纯果乐抓电子游艺规则,古纯果乐抓电子游戏技巧*****
Comments
Post a Comment